Diodes

Both p-type and n-type silicon will conduct electricity just like any conductor; however, if a piece of silicon is doped p-type in one section and n-type in an adjacent section, current will flow in only one direction across the junction between the two regions. This device is called a diode and is one of the most basic semiconductor devices.

A diode is called forward biased if it has a positive voltage across it from from the p- to n-type material. In this condition, the diode acts rather like a good conductor, and current can flow, as in Fig. 4.13.

  

Figure 4.13: A Forward Biased Diode

There will be a small voltage across the diode, about 0.6 volts for Si, and this voltage will be largely independent of the current, very different from a resistor.
If the polarity of the applied voltage is reversed, then the diode will be reverse biased and will appear nonconducting (Fig. 4.14). Almost no current will flow and there will be a large voltage across the device.

  

Figure 4.14: A Reverse Biased Diode

The non-symmetric behavior is due to the detailed properties of the pn-junction. The diode acts like a one-way valve for current and this is a very useful characteristic. One application is to convert alternating current (AC), which changes polarity periodically, into direct current (DC), which always has the same polarity. Normal household power is AC while batteries provide DC, and converting from AC to DC is called rectification. Diodes are used so commonly for this purpose that they are sometimes called rectifiers, although there are other types of rectifying devices. Figure 4.15 shows the input and output current for a simple half-wave

  

Figure 4.15: A Half-Wave Rectifier

rectifier. The circuits gets its name from the fact that the output is just the positive half of the input waveform. A full-wave rectifier circuit (shown in Figure 4.16) uses four diodes arranged so that both polarities of the input waveform can be used at the output.

  

Figure 4.16: A Full-Wave Rectifier

The full-wave circuit is more efficient than the half-wave one.

Silicon

Semiconductor devices are made primarily of silicon (silicon's element symbol is "Si"). Pure silicon forms rigid crystals because of its four valence (outermost) electron structure -- one Si  atom bonds to four other Si atoms forming a very regularly shaped diamond pattern. Figure 4.10 shows part of a silicon crystal structure.

  

Figure 4.10: A Silicon Crystal Structure

Pure silicon is not a conductor because there are no free electrons; all the electrons are tightly bound to neighboring atoms. To make silicon conducting, producers combine or "dope" pure silicon with very small amounts of other elements like boron or phosphorus. Phosphorus has five outer valence electrons. When three silicon atoms and one phosphorus atom bind together in the basic silicon crystal cell of four atoms, there is an extra electron and a net negative charge. Figure4.11 shows the crystal structure of phosphorus doped silicon.

  

Figure 4.11: Silicon Doped with Phosphorus

This type of material is called n-type silicon. The extra electron in the crystal cell is not strongly attached and can be released by normal thermal energy to carry current; the conductivity depends on the amount of phosphorus added to the silicon.
Boron has only three valance electrons. When three silicon atoms and one boron atom bind with each other there is a "hole" where another electron would be if the boron atom were silicon; see Fig. 4.12. This gives the crystal cell a positive net charge (referred to as p-type silicon), and the ability to pick up an electron easily from a neighboring cell.

  

Figure 4.12: Silicon Doped with Boron

The resulting migration of electron vacancies or holes acts like a flow of positive charge through the crystal and can support a current. It is sometimes convenient to refer to this current as a flow of positive holes, but in fact the current is really the result of electrons moving in the opposite direction from vacancy to vacancy.

Semiconductor Devices

The Truth About Charge   

Our statements above about charge are not wrong, but they are simple and incomplete. In order to understand how semiconductor devices work one needs a more complete description of the nature of charge in the real world. Charge does not exist independently; it is carried by subatomic particles. For this discussion we will be concerned primarily with electrons, which carry a negative charge of $1.6\; 10$^-19 C , the minimum amount of charge that can exist in isolation. At least, no one has found any smaller amount than this fundamental quantum of charge.
Electrons are one component of atoms and molecules. Atoms are the building blocks out of which all matter is constructed. Atoms bond with each other to form substances. Substances composed of just one type of atom are called elements. For example, copper, gold and silver are all elements; that is, each of them consists of only one type of atom. More complex substances are made up of more than one atom and are known as compounds. Water, which has both hydrogen and oxygen atoms, is such a compound. The smallest unit of a compound is a molecule. A water molecule, for example, contains two hydrogen atoms and one oxygen atom.
Atoms themselves are made up of even smaller components: protons, neutrons and electrons. Protons and neutrons form the nucleus of an atom, while the electrons orbit the nucleus. Protons carry positive charge and electrons carry negative charge; the magnitude of the charge for both particles is the same, one quantum charge, $1.6\; �10$^-19 C . Neutrons are not charged. Normally, atoms have the same number of protons and electrons and have no net electrical charge.

  

Figure 4.8: Structure of an Atom

Electrons that are far from the nucleus are relatively free to move around under the influence of external fields because the force of attraction from the positive charge in the nucleus is weak at large distances. In fact, it takes little force in many cases to completely remove an outer electron from an atom, leaving an ion with a net positive charge. Once free, electrons can move at speeds approaching the speed of light (roughly 670 million miles per hour) through metals, gases and vacuum. They can also become attached to another atom, forming an ion with net negative charge.
Electric current in metal conductors consists of a flow of free electrons. Because electrons have negative charge, the flow of electrons is in a direction opposite to the positive current. Free electrons traveling through a conductor drift until they hit other electrons attached to atoms. These electrons are then dislodged from their orbits and replaced by the formerly free electrons. The newly freed electrons then start the process anew. At the microscopic level, electron flow through a conductor is not a steady stream, like water flowing from a faucet, but rather a series of short bursts.

  

Figure 4.9: A Simple Model of Electron Flow

Batteries    

Charges can be separated by several means to produce a voltage. A battery uses a chemical reaction to produce energy and separate opposite sign charges onto its two terminals. As the charge is drawn off by an external circuit, doing work and finally returning to the opposite terminal, more chemicals in the battery react to restore the charge difference and the voltage. The particular type of chemical reaction used determines the voltage of the battery, but for most commercial batteries the voltage is about 1.5 V per chemical section or cell. Batteries with higher voltages really contain multiple cells inside connected together in series. Now you know why there are 3 V, 6 V, 9 V, and 12 V batteries, but no 4 or 7 V batteries. The current a battery can supply depends on the speed of the chemical reaction supplying charge, which in turn often depends on the physical size of the cell and the surface area of the electrodes. The size of a battery also limits the amount of chemical reactants stored. During use, the chemical reactants are depleted and eventually the voltage drops and the current stops. Even with no current flow, the chemical reaction proceeds at a very slow rate (and there is some internal current flow), so a battery has a finite storage or shelf life, about a year or two in most cases. In some types of batteries, like the ones we use for the robot, the chemical reaction is reversible: applying an external voltage and forcing a current through the battery, which requires work, reverses the chemical reaction and restores most, but not all, the chemical reactants. This cycle can be repeated many times. Batteries are specified in terms of their terminal voltage, the maximum current they can deliver, and the total current capacity in ampere-hours.

You should handle batteries carefully, especially the ones we use in this course. Chemicals are a very efficient and compact way of storing energy. Just consider the power of gasoline or explosives, or the fact that you can play soccer for several hours powered only by a slice of cold pizza for breakfast. Never connect the terminals of a battery together with a wire or other good conductor. The battery we use for the RoboBoard is similar to the battery in cars, which uses lead and sulphuric acid as reactants. Such batteries can deliver very large currents through a short circuit, hundreds of  amperes. The large current will heat the wire and possibly burn you; the resulting rapid internal chemical reactions also produce heat and the battery can explode, spreading nasty, reactive chemicals about. Charging these batteries with too large a current can have the same effect. Double check the circuit and instructions before connecting a battery to any circuit. 

Current

Charge is mobile and can flow freely in certain materials, called conductors. Metals and a few other elements and compounds are conductors. Materials that charge cannot flow through are called insulators. Air, glass, most plastics, and rubber are insulators, for example. And then there are some materials called semiconductors, that, historically, seemed to be good conductors sometimes but much less so other times. Silicon and germanium are two such materials. Today, we know that the difference in electrical behavior of different samples of these materials is due to extremely small amounts of impurities of different kinds, which could not be measured earlier. This recognition, and the ability to precisely control the "impurities" has led to the massive semiconductor electronics industry and the near-magical devices it produces, including those on your RoboBoard. 

Imagine two oppositely charged bodies, say metal spheres, that are being held apart, as in Fig. 4.3.

  

Figure 4.3: Two spheres with opposite charges are connected by a conductor, allowing charge to flow.

There is a force between them, the potential for work, and thus a voltage. Now we connect a conductor between them, a metal wire. On the positively charged sphere, positive charges rush along the wire to the other sphere, repelled by the nearby similar charges and attracted to the distant opposite charges. The same thing occurs on the other sphere and negative charge flows out on the wire. Positive and negative charges combine to neutralize each other, and the flow continues until there are no charge differences between any points of the entire connected system. There may be a net residual charge if the amounts of original positive and negative charge were not equal, but that charge will be distributed evenly so all the forces are balanced. If they were not, more charge would flow. The charge flow is driven by voltage or potential differences. After things have quieted down, there is no voltage difference between any two points of the system and no potential for work. All the work has been done by the moving charges heating up the wire.

The flow of charge is called electrical current. Current is measured in amperes (a), amps for short (named after another French scientist who worked mostly with magnetic effects). An ampere is defined as a flow of one Coulomb of charge in one second past some point. While a Coulomb is a lot of charge to have in one place, an ampere is a common amount of current; about one ampere flows through a 100 watt incandescent light bulb, and a stove burner or a large motor would require ten or more amperes. On the other hand low power digital circuits use only a fraction of an ampere, and so we often use units of $1/1000$ of an ampere, a milliamp, abbreviated as ma, and even $1/1000$ of a milliamp, or a microamp, $a$ . The currents on the RoboBoard are generally in the milliamp range, except for the motors, which can require a full ampere under heavy load. Current has a direction, and we define a positive current from point $A$ to $B$ as the flow of positive charges in the same direction. Negative charges can flow as well, in fact, most current is actually the result of negative charges moving. Negative charges flowing from $A$ to $B$ would be a negative current, but, and here is the tricky part, negative charges flowing from $B$ to $A$ would represent a positive current from $A$ to $B$ . The net effect is the same: positive charges flowing to neutralize negative charge or negative charges flowing to neutralize positive charge; in both cases the voltage is reduced and by the same amount.

Voltage

 

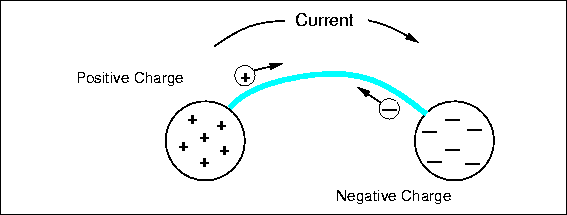
First we return to the basic assumption that forces are the result of charges. Specifically, bodies with opposite charges attract, they exert a force on each other pulling them together. The magnitude of the force is proportional to the product of the charge on each mass. This is just like gravity, where we use the term "mass" to represent the quality of bodies that results in the attractive force that pulls them together (see Fig. 4.1).

  

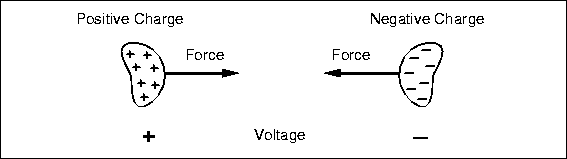
Figure 4.1: Opposite charges exert an attractive force on each other, just like two masses attract. External force is required to hold them apart, and work is required to move them farther apart.

Electrical force, like gravity, also depends inversely on the distance squared between the two bodies; short separation means big forces. Thus it takes an opposing force to keep two charges of opposite sign apart, just like it takes force to keep an apple from falling to earth. It also takes work and the expenditure of energy to pull positive and negative charges apart, just like it takes work to raise a big mass against gravity, or to stretch a spring. This stored or potential energy can be recovered and put to work to do some useful task. A falling mass can raise a bucket of water; a retracting spring can pull a door shut or run a clock. It requires some imagination to devise ways one might hook on to charges of opposite sign to get some useful work done, but it should be possible.
The potential that separated opposite charges have for doing work if they are released to fly together is called voltage, measured in units of volts (V). (Sadly, the unit volt is not named for Voltaire, but rather for Volta, an Italian scientist.) The greater the amount of charge and the greater the physical separation, the greater the voltage or stored energy. The greater the voltage, the greater the force that is driving the charges together. Voltage is always measured between two points, in this case, the positive and negative charges. If you want to compare the voltage of several charged bodies, the relative force driving the various charges, it makes sense to keep one point constant for the measurements. Traditionally, that common point is called "ground."
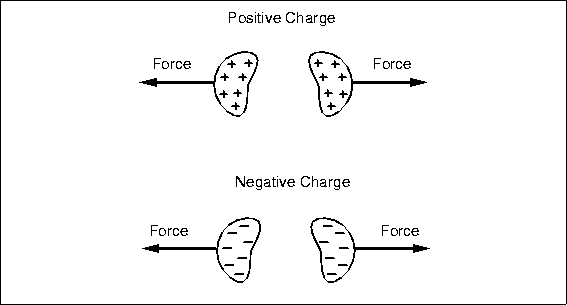
Early workers, like Coulomb, also observed that two bodies with charges of the same type, either both positive or both negative, repelled each other (Fig. 4.2). They experience a force pushing

  

Figure 4.2: Like charges exert a repulsive force on each other. External force is required to hold them together, and work is required to push them closer.

them apart, and an opposing force is necessary to hold them together, like holding a compressed spring. Work can potentially be done by letting the charges fly apart, just like releasing the spring. Our analogy with gravity must end here: no one has observed negative mass, negative gravity, or uncharged bodies flying apart unaided. Too bad, it would be a great way to launch a space probe. The voltage between two separated like charges is negative; they have already done their work by running apart, and it will take external energy and work to force them back together.

So how do you tell if a particular bunch of charge is positive or negative? You can't in isolation. Even with two charges, you can only tell if they are the same (they repel) or opposite (they attract). The names are relative; someone has to define which one is "positive." Similarly, the voltage between two points $A$ and $B$ , $V$_AB , is relative. If $V$_AB is positive you know the two points are oppositely charged, but you cannot tell if point $A$ has positive charge and point $B$ negative, or visa versa. However, if you make a second measurement between $A$ and another point $C$ , you can at least tell if $B$ and $C$ have the same charge by the relative sign of the two voltages, $V$_AB and $V$_ACto your common point $A$ . You can even determine the voltage between $B$ and $C$ without measuring it: $V$_BC = V_AC - V_AB . This is the advantage of defining a common point, like $A$ , as ground and making all voltage measurements with respect to it. If one further defines the charge at point $A$ to be negative charge, then a positive $V$_AB means point $B$ is positively charged, by definition. The names and the signs are all relative, and sometimes confusing if one forgets what the reference or ground point is.

Charge

No one knows what charge really is anymore than anyone knows what gravity is. Both are models, constructions, fabrications if you like, to describe and represent something that can be measured in the real world, specifically a force. Gravity is the name for a force between masses that we can feel and measure. Early workers observed that bodies in "certain electrical condition" also exerted forces on one another that they could measure, and they invented charge to explain their observations. Amazingly, only three simple postulates or assumptions, plus some experimental observations, are necessary to explain all electrical phenomena. Everything: currents, electronics, radio waves, and light. Not many things are so simple, so it is worth stating the three postulates clearly.

Charge exists.    

We just invent the name to represent the source of the physical force that can be observed. The assumption is that the more charge something has, the more force will be exerted. Charge is measured in units of Coulombs, abbreviated C. The unit was named to honor Charles Augustin Coulomb (1736-1806) the French aristocrat and engineer who first measured the force between charged objects using a sensitive torsion balance he invented. Coulomb lived in a time of political unrest and new ideas, the age of Voltaire and Rousseau. Fortunately, Coulomb completed most of his work before the revolution and prudently left Paris with the storming of the Bastille.

Charge comes in two styles.

We call the two styles positive charge, $+$ , and (you guessed it) negative charge, $-$ . Charge also comes in lumps of $1.6\; �10$^-19C , which is about two ten-million-trillionths of a Coulomb. The  discrete nature of charge is not important for this discussion, but it does serve to indicate that a Coulomb is a LOT of charge.

Charge is conserved.

You cannot create it and you cannot annihilate it. You can, however, neutralize it. Early workers observed experimentally that if they took equal amounts of positive and negative charge and combined them on some object, then that object neither exerted nor responded to electrical forces; effectively it had zero net charge. This experiment suggests that it might be possible to take uncharged, or neutral, material and to separate somehow the latent positive and negative charges. If you have ever rubbed a balloon on wool to make it stick to the wall, you have separated charges using mechanical action.

Those are the three postulates. Now we will present some of the experimental findings that both led to them and amplify their significance.

Inductor

   An inductor, also called a coil or reactor, is a passive two-terminal electrical component which resists changes in electric current passing through it. It consists of a conductor such as a wire, usually wound into a coil. Energy is stored in a magnetic field in the coil as long as current flows. When the current flowing through an inductor changes, the time-varying magnetic field induces a voltage in the conductor, according to Faraday’s law of electromagnetic induction. According to Lenz's law, the direction of induced electromotive force (or "e.m.f.") is always such that it opposes the change in current that created it. As a result, inductors always oppose a change in current, in the same way that a flywheel opposes a change in rotational velocity. Care should be taken not to confuse this with the resistance provided by a resistor.
An inductor is characterized by its inductance, the ratio of the voltage to the rate of change of current, which has units of henries (H). Inductors have values that typically range from 1 µH (10⁻⁶H) to 1 H. Many inductors have a magnetic core made of iron or ferrite inside the coil, which serves to increase the magnetic field and thus the inductance. Along with capacitors and resistors, inductors are one of the three passive linear circuit elements that make up electric circuits. Inductors are widely used in alternating current (AC) electronic equipment, particularly in radio equipment. They are used to block AC while allowing DC to pass; inductors designed for this purpose are called chokes. They are also used in electronic filters to separate signals of different frequencies, and in combination with capacitors to make tuned circuits, used to tune radio and TV receivers.


               

Resistance

Resistance is the opposition that a substance offers to the flow of electric current.  It is represented by the uppercase letter R.  The standard unit of resistance is the ohm, sometimes written out as a word, and sometimes symbolized by the uppercase Greek letter omega:

When an electric current of one ampere passes through a component across which a potential difference (voltage) of one volt exists, then the resistance of that component is one ohm. (For more discussion of the relationship among current, resistance and voltage, see Ohm's law.)

 Ohm's law:
Ohm's law states that the current through a conductor between two points is directly proportional to the voltage across the two points. Introducing the constant of proportionality, the resistance, one arrives at the usual mathematical equation that describes this relationship

${\displaystyle I={\frac {V}{R}},}$

where I is the current through the conductor in units of amperes, V is the voltage measured across the conductor in units of volts, and R is the resistance of the conductor in units of ohms. More specifically, Ohm's law states that the R in this relation is constant, independent of the current.
The law was named after the German physicist Georg Ohm, who, in a treatise published in 1827, described measurements of applied voltage and current through simple electrical circuits containing various lengths of wire. He presented a slightly more complex equation than the one above  to explain his experimental results. The above equation is the modern form of Ohm's law.
In physics, the term Ohm's law is also used to refer to various generalizations of the law originally formulated by Ohm. The simplest example of this is:

${\displaystyle \mathbf {J} =\sigma \mathbf {E} ,}$

where J is the current density at a given location in a resistive material, E is the electric field at that location, and σ (Sigma) is a material-dependent parameter called the conductivity. This reformulation of Ohm's law is due to Gustav Kirchhoff

Capacitance

WHAT IS CAPACITANCE?

An electrical parameter which physically is most easy to define, electrically often misconstrued.

Physically, a capacitor is two electrical conductors separated by a non-conducting (or very high resistance) medium between the conductors. Consider the two plates of area (A) in Figure 1. The plates are metallic and they are separated by a distance (D).

Figure 1.

C=KA/D

If we fill the space between the plates with a conductor (water, acid, etc.) and close the switch (S), we get a current dictated by ohms law, I=v/r (where V is voltage, and R is the resistance between the plates). If the space is a non-conductor, no current will flow but the voltage will exist across the plates. The plus side and the negative side attract, and electrical charges will exist on the plates; thus an electrical field will exist in the space between. Clearly, the larger the plates, the more charges will exist and the closer the plates (D), the stronger the electrical attraction between the plates will be.

If we now reverse the polarity of the battery, the plus plate is now negative and the negative plate plus. For the electrical charge to reverse, ¢ electrons¢ must have flowed, reversing their position. Since ¢ electron flow¢ is current, we have current flow when we reverse the polarity.

If we now substitute the battery with an alternating current source, the polarity will reverse every 1/2 cycle and we will, hence, get continuous current flow. Therefore, while a capacitor will not allow DC current to flow through, AC current can pass. The amount of current will depend on the supply voltage, the capacity of the plates to hold charges and the distance (D), which determines the leakage (or electrical field) in the space and the material between the plates.

Figure 2.

The formula for current flow through a capacitor with an alternating voltage applied is I=V2 FKA/D. K is defined as the dielectric of material or ability to store electrons.

Note: - the higher the area A, the larger the current

- the smaller the D, the larger the current

- K is determined by the material having a high value (eg. water = 80) and non-conducting materials having a lower value (eg. air = 1). Current is increased with the supply frequency (f), as you are reversing the charges more frequently and current increases with supply voltage.

Electromagnetics

Elements of vector calculus: divergence and curl; Gauss law and stokes theorem, Maxewell's equation: differential and integral forms.Wave equation, Poynting vector. Plane waves: propagation through various media; reflection and refraction; phase and group velocity; skin depth. Transmission lines: characteristic impedance; impedance transformation;Smith chart; impedance matching; pulse excitation. Waveguides: modes in rectangular waveguides; boundary conditionds; cut-off frequencies; dispersion relations. Antennas: Dipole antennas; antenna arrays; radiation pattern; reciprocity theorem,antenna gain.

 GAUSS LAW:
    The total of the electric flux out of a closed surface is equal to the magnitude of the charge enclosed divided by the permittivity of free space. As a mathematical equation, it looks like this

 

PRINTED CIRCUIT BOARD

Subfields

Electronic engineering has many subfields. This section describes some of the most popular subfields in electronic engineering; although there are engineers who focus exclusively on one subfield, there are also many who focus on a combination of subfields.
Signal processing deals with the analysis and manipulation of signals. Signals can be either analog, in which case the signal varies continuously according to the information, or digital, in which case the signal varies according to a series of discrete values representing the information.
For analog signals, signal processing may involve the amplification and filtering of audio signals for audio equipment or the modulation and demodulation of signals for telecommunications. For digital signals, signal processing may involve the compression, error checking and error detection of digital signals.
Telecommunications engineering deals with the transmission of information across a channel such as a co-axial cable, optical fiber or free space.
Transmissions across free space require information to be encoded in a carrier wave in order to shift the information to a carrier frequency suitable for transmission, this is known as modulation. Popular analog modulation techniques include amplitude modulation and frequency modulation. The choice of modulation affects the cost and performance of a system and these two factors must be balanced carefully by the engineer.
Once the transmission characteristics of a system are determined, telecommunication engineers design the transmitters and receivers needed for such systems. These two are sometimes combined to form a two-way communication device known as a transceiver. A key consideration in the design of transmitters is their power consumption as this is closely related to their signal strength. If the signal strength of a transmitter is insufficient the signal's information will be corrupted by noise.
Control engineering has a wide range of applications from the flight and propulsion systems of commercial airplanes to the cruise control present in many modern cars. It also plays an important role in industrial automation.
Control engineers often utilize feedback when designing control systems. For example, in a car with cruise control the vehicle's speed is continuously monitored and fed back to the system which adjusts the engine's power output accordingly. Where there is regular feedback, control theory can be used to determine how the system responds to such feedback.
Instrumentation engineering deals with the design of devices to measure physical quantities such as pressure, flow and temperature. These devices are known as instrumentation.
The design of such instrumentation requires a good understanding of physics that often extends beyond electromagnetic theory. For example, radar guns use the Doppler effect to measure the speed of oncoming vehicles. Similarly, thermocouples use the Peltier–Seebeck effect to measure the temperature difference between two points.
Often instrumentation is not used by itself, but instead as the sensors of larger electrical systems. For example, a thermocouple might be used to help ensure a furnace's temperature remains constant. For this reason, instrumentation engineering is often viewed as the counterpart of control engineering.
Computer engineering deals with the design of computers and computer systems. This may involve the design of new computer hardware, the design of PDAs or the use of computers to control an industrial plant. Development of embedded systems—systems made for specific tasks (e.g., mobile phones)—is also included in this field. This field includes the micro controller and its applications. Computer engineers may also work on a system's software. However, the design of complex software systems is often the domain of software engineering, which is usually considered a separate discipline.
VLSI design engineering VLSI stands for very large scale integration. It deals with fabrication of ICs and various electronics components.

Electronics

In the field of electronic engineering, engineers design and test circuits that use the electromagnetic properties of electrical components such as resistors,capacitors, inductors, diodes and transistors to achieve a particular functionality. The tuner circuit, which allows the user of a radio to filter out all but a single station, is just one example of such a circuit.
In designing an integrated circuit, electronics engineers first construct circuit schematics that specify the electrical components and describe the interconnections between them. When completed, VLSI engineers convert the schematics into actual layouts, which map the layers of various conductor and semiconductor materials needed to construct the circuit. The conversion from schematics to layouts can be done by software but very often requires human fine-tuning to decrease space and power consumption. Once the layout is complete, it can be sent to a fabrication plant for manufacturing.
For systems of intermediate complexity engineers may use VHDL modelling for programmable logic devices and FPGAs
Integrated circuits, FPGAs and other electrical components can then be assembled on printed circuit boards to form more complicated circuits. Today, printed circuit boards are found in most electronic devices including televisions, computers and audio players.

Goals

 Its goals are to excite students about the study of electrical and computer engineering by exposing them early in their education to electrical components and their application in systems, and to enhance their problem solving skills through analysis and design.

Topics

• Introduction
• DC circuits
• Electromagnets, DC motors
• Electronics: Diodes, Transistors
• Sensors, feedback and control
• Digital logic
• Pulse width modulation and communication
• Basic computer organization

Important subjects

ECE Related Core subjects

Electronic Circuits and Devices
Electrical Circuit Analysis
Probability Theory and Stochastic Process
Switching Theory and Logic Design
Digital Signal Processing
Digital Electronics
Signals and Systems
Digital Communication
Microprocessor and Microcontroller
Transmission Lines and Waveguides
Electromagnetic Field
 Wireless Communication
Digital Image Processing
Antenna and Wave Propagation
VLSI
Embedded System